Zadanie nr 8761365
Bok rombu ma długość 13 cm, a jedna z przekątnych ma długość 24 cm. Oblicz pole tego rombu.
Rozwiązanie
Przekątne rombu dzielą się na połowy i są prostopadłe.
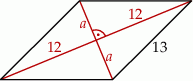
To oznacza, że romb składa się z 4 przystających trójkątów prostokątnych. Korzystając z twierdzenia Pitagorasa obliczmy długość drugiej przyprostokątnej takiego trójkąta.
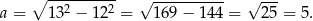
Pole rombu jest więc równe
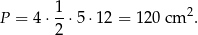
Odpowiedź: