Zadanie nr 9213186
Oblicz miary kątów środkowych 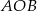 zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego
zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego 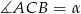 .
.
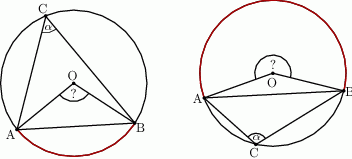
Rozwiązanie
Dorysujmy promień 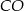 i oznaczmy przez
i oznaczmy przez 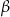 i
i 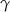 miary kątów na jakie promień ten podzielił kąt
miary kątów na jakie promień ten podzielił kąt 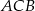 . W szczególności
. W szczególności 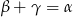 .
.
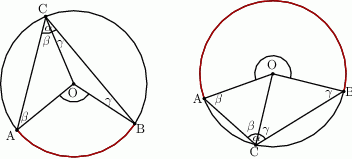
Zauważmy, że każdy z trójkątów 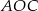 i
i 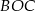 jest równoramienny, więc
jest równoramienny, więc 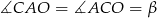 i
i 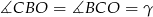 . Sumy kątów w trójkątach
. Sumy kątów w trójkątach 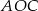 i
i 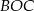 są równe
są równe 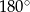 , zatem
, zatem
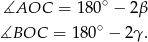
To oznacza, że szukany kąt środkowy 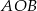 ma miarę
ma miarę
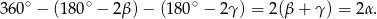
Odpowiedź: