Zadanie nr 9298444

Prostokąt 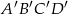′ ′ ′ ′ A B C D jest podobny do prostokąta 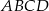ABCD w skali 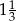1 1 3 . Pole prostokąta 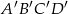A′B ′C ′D ′ jest równe 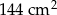144 cm 2 . Krótszy bok prostokąta 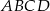ABCD ma długość 6 cm. Oblicz długości pozostałych boków tych prostokątów.

Rozwiązanie

Ponieważ skala podobieństwa jest równa 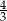4 3 , pole prostokąta 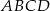ABCD spełnia

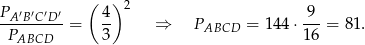
( ) 2 PA-′B′C′D′ 4- 9-- PABCD = 3 ⇒ PABCD = 14 4⋅ 16 = 81.

Zatem drugi bok prostokąta 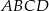ABCD ma długość

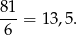
81- 6 = 1 3,5.

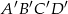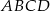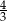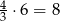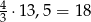Aby otrzymać długości boków prostokąta A ′B′C′D ′ , trzeba pomnożyć długości boków prostokąta ABCD przez 4 3 . Są on więc równe 4 ⋅6 = 8 3 i 4 3 ⋅13,5 = 18 .
Odpowiedź: 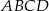ABCD : 6 cm, 13,5 cm, 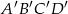A ′B ′C ′D′ : 8 cm, 18 cm