/Szkoła podstawowa/Geometria

Zadanie nr 9628769

Dodaj do ulubionych
Dodaj do rozwiązanych

Narysuj w układzie współrzędnych czworokąt o wierzchołkach: 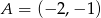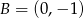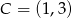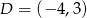A = (−2 ,−1 ) , B = (0,− 1) , C = (1,3) , D = (− 4,3) , a następnie oblicz jego pole i obwód.

Rozwiązanie

Zaznaczamy dane punkty w układzie współrzędnych.

PIC

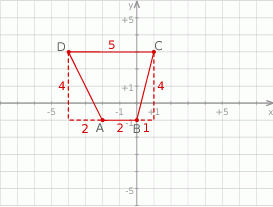
Otrzymany czworokąt to trapez o podstawach długości 2 i 5, oraz wysokości równej 4. Jego pole jest więc równe

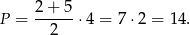
P = 2+--5-⋅4 = 7 ⋅2 = 14. 2

Aby obliczyć obwód tego trapezu korzystamy z twierdzenia Pitagorasa w trójkątach prostokątnych zaznaczonych przerywanymi liniami.

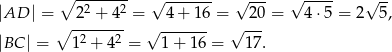
∘ ------- √ ------- √ --- √ ---- √ -- |AD | = 22 + 42 = 4 + 16 = 2 0 = 4⋅ 5 = 2 5, ∘ ------- √ ------- √ --- |BC | = 12 + 42 = 1 + 16 = 17.

Obwód trapezu jest więc równy

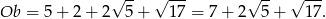
√ -- √ --- √ -- √ --- Ob = 5+ 2+ 2 5+ 17 = 7 + 2 5 + 1 7.

 
Odpowiedź: Pole: 14, obwód: 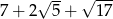√ -- √ --- 7 + 2 5 + 17 .

Wersja PDF