/Szkoła podstawowa/Geometria

Zadanie nr 9653108

Dodaj do ulubionych
Dodaj do rozwiązanych

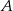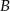Przez punkty A i B okręgu poprowadzono styczne, które przecięły się w punkcie C .

PIC

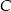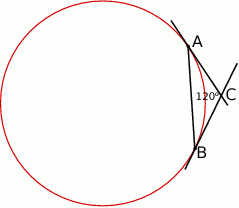
Wykaż, że jeżeli 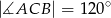|∡ACB | = 12 0∘ , to cięciwa 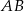AB ma długość równą długości promienia okręgu.

Rozwiązanie

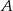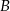Połączmy punkty A i B ze środkiem okręgu S .

PIC

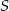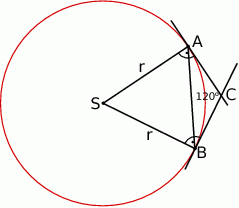
Ponieważ promień łączący środek okręgu z punktem styczności jest prostopadły do stycznej, dwa kąty czworokąta 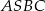ASBC są proste. W takim razie

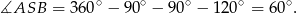
∡ASB = 36 0∘ − 9 0∘ − 90∘ − 120∘ = 60 ∘.

Patrzymy teraz na trójkąt 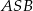ASB – jest on równoramienny oraz kąt między jego ramionami jest równy 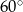∘ 60 . Jest to więc trójkąt równoboczny. W szczególności

AB = SB = SA = r.
Wersja PDF