Zadanie nr 9787403

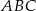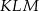Uzasadnij, że trójkąty ABC i KLM przedstawione na rysunku są podobne.

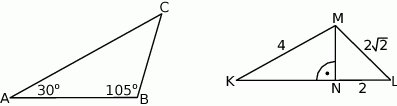
Rozwiązanie

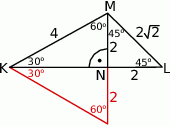
Patrzymy najpierw na trójkąt 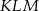KLM – korzystając z twierdzenia Pitagorasa obliczamy długość odcinka .

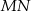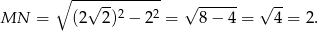
∘ --√---------- √ ------ √ -- MN = (2 2)2 − 22 = 8 − 4 = 4 = 2.

To oznacza, że trójkąt 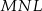MNL jest połówką kwadratu, a trójkąt 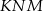KNM jest połówką trójkąta równobocznego.

Możemy więc obliczyć miary kątów trójkąta 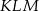KLM .

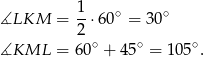
∡LKM = 1-⋅6 0∘ = 30∘ 2 ∡KML = 60 ∘ + 4 5∘ = 105∘.

To oznacza, że trójkąty mają takie same miary dwóch kątów wewnętrznych – są więc podobne.

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz