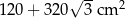/Szkoła podstawowa/Geometria

Zadanie nr 9799471

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz pole powierzchni całkowitej i objętość prostopadłościanu 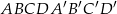ABCDA ′B′C′D ′ , w którym krawędź 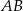AB ma długość 10 cm i tworzy z przekątną 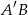A ′B ściany bocznej kąt 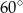60∘ , a krawędź 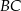BC jest o cztery centymetry krótsza od krawędzi AB .

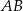Rozwiązanie

Zaczynamy od rysunku.

PIC

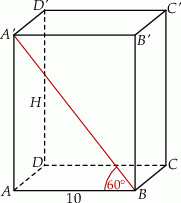
Z podanych danych wiemy, że 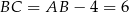BC = AB − 4 = 6 , czyli pozostało nam obliczyć długość wysokości 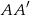AA ′ . Z trójkąta prostokątnego 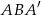ABA ′ mamy

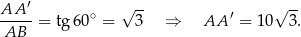
AA--′ ∘ √ -- ′ √ -- AB = tg6 0 = 3 ⇒ AA = 10 3.

Możemy teraz obliczyć objętość i pole powierzchni.

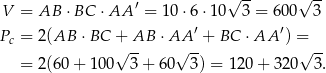
√ -- √ -- V = AB ⋅BC ⋅AA ′ = 10 ⋅6⋅ 10 3 = 600 3 ′ ′ Pc = 2(AB ⋅BC +√ -AB ⋅ AA√ -+ BC ⋅AA ) =√-- = 2(60 + 100 3 + 6 0 3) = 120 + 32 0 3.

 
Odpowiedź: Objętość: 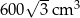√ -- 3 60 0 3 cm , pole powierzchni: √ -- 120 + 32 0 3 cm 2

Wersja PDF