Zadanie nr 9911142
Powierzchnię boczną pudełka w kształcie graniastosłupa czworokątnego rozcięto wzdłuż przekątnych dwóch przeciwległych ścian bocznych i otrzymano dwa przystające trapezy. Podstawy otrzymanych trapezów mają długości 16 cm i 34 cm, a ich ramiona mają długość 15 cm. Oblicz objętość tego pudełka. Zapisz obliczenia.
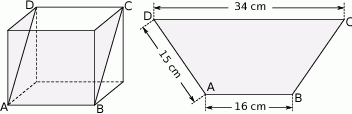
Rozwiązanie
Dorysujmy wysokości trapezu.
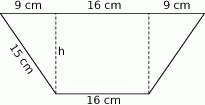
Zauważmy, że długości krawędzi podstawy graniastosłupa są równe 16 cm (krótsza podstawa trapezu) oraz 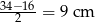 . Wysokość graniastosłupa jest równa wysokości trapezu – obliczamy ją z twierdzenia Pitagorasa.
. Wysokość graniastosłupa jest równa wysokości trapezu – obliczamy ją z twierdzenia Pitagorasa.
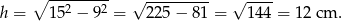
Pozostało obliczyć objętość graniastosłupa.
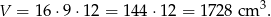
Odpowiedź: