/Studia/Algebra liniowa/Liniowa niezależność/Abstrakcyjna

Zadanie nr 3971717

Dodaj do ulubionych
Dodaj do rozwiązanych

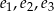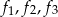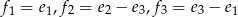Wiedząc, że wektory e1,e2,e3 są liniowo niezależne sprawdź liniową niezależność wektorów f1,f2,f3 jeżeli f1 = e1,f2 = e2 − e3,f3 = e3 − e1 .

Rozwiązanie

Przypuśćmy, że kombinacja linowa wektorów jest równa 0:

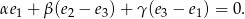
αe1 + β (e2 − e3)+ γ(e3 − e1) = 0.

Musimy pokazać, że 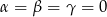α = β = γ = 0 . Przekształcamy

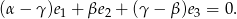
(α− γ)e1 + βe2 + (γ − β)e3 = 0.

Ponieważ wektory 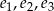e1,e2,e3 są liniowo niezależne, współczynniki tej kombinacji muszą być zerowe.

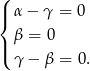
( |{ α− γ = 0 | β = 0 ( γ − β = 0 .

Z tego układu łatwo wynika, że 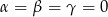α = β = γ = 0 .  
Odpowiedź: Układ jest liniowo niezależny.

Wersja PDF