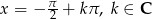Zadanie nr 1379379
Rozwiąż równanie 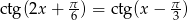 .
.
Rozwiązanie
Wyznaczamy najpierw dziedzinę równania
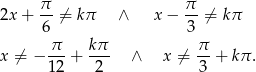
Będziemy teraz korzystać z warunku (który łatwo odczytać z wykresu)
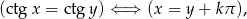
gdzie 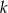 jest liczbą całkowitą.
jest liczbą całkowitą.
Liczymy
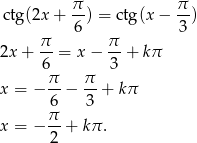
Odpowiedź: 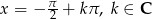
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 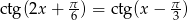 .
.
Wyznaczamy najpierw dziedzinę równania
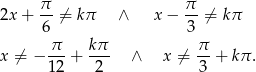
Będziemy teraz korzystać z warunku (który łatwo odczytać z wykresu)
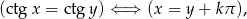
gdzie 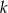 jest liczbą całkowitą.
jest liczbą całkowitą.
Liczymy
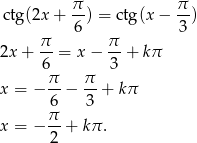
Odpowiedź: