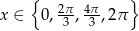/Szkoła średnia/Równania/Trygonometryczne/Z tangensem

Zadanie nr 2223817

Rozwiąż równanie 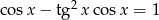2 cos x− tg x cosx = 1 w przedziale ⟨0 ,2 π⟩ .

Wersja PDF

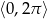Rozwiązanie

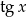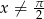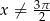Ze względu na tg x musi być π- x ⁄= 2 i 3π- x ⁄= 2 . Przekształcamy równanie

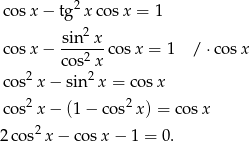
2 co sx − tg x cos x = 1 sin2 x co sx − ---2-- cosx = 1 / ⋅cos x 2 cos 2x co s x − sin x = cosx co s2x − (1− cos2x ) = cosx 2co s2x − cos x− 1 = 0.

Podstawiamy teraz 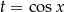t = cosx .

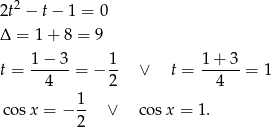
2t2 − t− 1 = 0 Δ = 1 + 8 = 9 1−--3- 1- 1-+-3- t = 4 = − 2 ∨ t = 4 = 1 1 cosx = − -- ∨ co sx = 1 . 2

Teraz szkicujemy kawałek cosinusa (na przedziale 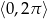⟨0,2π ⟩ ).

PIC

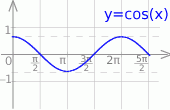
Z wykresu odczytujemy rozwiązania.

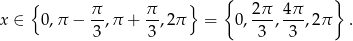
{ } { } x ∈ 0,π − π-,π + π-,2π = 0, 2-π, 4π-,2π . 3 3 3 3

 
Odpowiedź: { } x ∈ 0, 2π-, 4π,2π 3 3

Wersja PDF