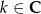/Szkoła średnia/Równania/Trygonometryczne/Z tangensem

Zadanie nr 2957973

Wyznacz wszystkie rozwiązania równania 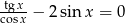tgx- cosx − 2sin x = 0 .

Wersja PDF

Rozwiązanie

Oczywiście musi być 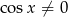cosx ⁄= 0 (ze względu na tg x ).

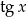Sposób I

Liczymy

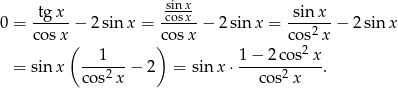
tgx sinx sin x 0 = ----- − 2 sin x = cosx-− 2sin x = ---2-- − 2 sin x co sx( )cosx cos2 x --1--- 1-−-2-cos-x- = sinx cos2 x − 2 = sinx ⋅ cos2 x .

Zatem 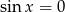sin x = 0 , czyli 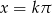x = kπ , gdzie 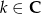k ∈ C lub

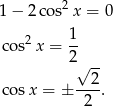
1 − 2 cos2x = 0 cos2x = 1- 2√ -- 2 cosx = ± ---. 2

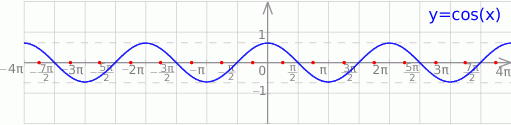
Rozwiązaniem tego ostatniego równania są liczby postaci 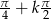π+ kπ- 4 2 , gdzie k ∈ C .

PIC

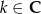Sposób II

Tym razem równanie przekształcamy tak, aby zostały same sinusy.

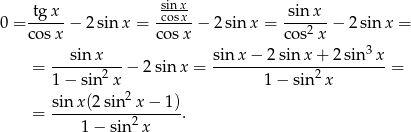
sinx- 0 = tg-x-− 2sinx = -cosx- − 2 sin x = sin-x-− 2 sinx = cosx cos x cos2x sin x sinx − 2 sinx + 2 sin 3x = ----------− 2 sinx = ------------------------= 1− sin 2x 1 − sin 2x sinx (2 sin2x − 1 ) = -----------2------. 1 − sin x

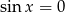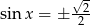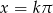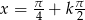Zatem sin x = 0 lub √-2 sinx = ± 2 . Pierwsza równość daje x = kπ , a druga π π x = 4-+ k 2- .  
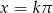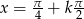Odpowiedź: x = kπ lub x = π4 + kπ2- , gdzie k ∈ C

Wersja PDF