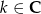Zadanie nr 3161770

Rozwiąż równanie 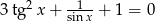2 -1-- 3tg x+ sinx + 1 = 0 .

Rozwiązanie

Przekształćmy podane równanie.

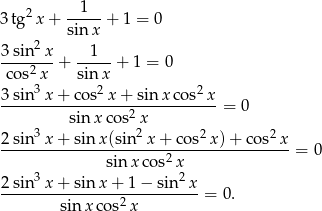
1 3tg2 x + -----+ 1 = 0 sinx 3-sin-2x- -1--- cos2x + sin x + 1 = 0 3 2 2 3-sin--x-+-cos--x+--sin-x-cos-x-= 0 sin xco s2x 2 sin 3x + sinx (sin 2x + cos2 x)+ cos2x -----------------------2----------------= 0 3 sin xco s x2 2-sin--x-+-sinx-+-1-−-sin--x = 0 . sin xcos2 x

Podstawmy 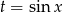t = sin x i mamy równanie

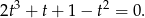
2t3 + t+ 1 − t2 = 0.

Szukamy wymiernych pierwiastków tego wielomianu wśród liczb postaci 1 q , gdzie 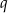dzieli 2. Okazuje się, że pierwiastkiem jest 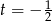t = − 1 2 . Dzielimy teraz wielomian przez dwumian 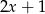2x+ 1 . My zrobimy to grupując wyrazy.

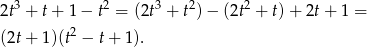
3 2 3 2 2 2t + t+ 1 − t = (2t + t )− (2t + t)+ 2t+ 1 = (2t+ 1)(t2 − t + 1).

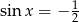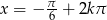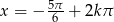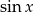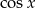Wielomian kwadratowy w nawiasie nie ma pierwiastków, więc dostajemy 1 sin x = − 2 . Stąd π- x = − 6 + 2kπ lub 5π- x = − 6 + 2kπ . Koniecznie trzeba jeszcze sprawdzić, czy te rozwiązania należą do dziedziny równania, ale w mianownikach mieliśmy sin x i co sx , więc dla 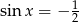wszystko jest ok.
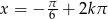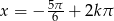Odpowiedź: x = − π6-+ 2kπ lub x = − 5π6-+ 2kπ , k ∈ C