Zadanie nr 3958690

Rozwiąż równanie 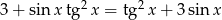2 2 3+ sin x tg x = tg x + 3sin x w przedziale ⟨0 ,2 π⟩ .

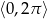Rozwiązanie

Sposób I

Przekształcamy równanie – przenosimy wszystko na jedną stronę i próbujemy coś wyłączyć przed nawias.

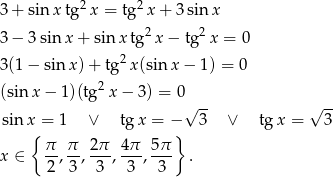
2 2 3 + sin xtg x = tg x + 3 sinx 3 − 3 sin x + sinx tg2x − tg 2x = 0 3(1 − sin x)+ tg 2x(sin x− 1) = 0 2 (sin x− 1)(tg x − 3) = 0√ -- √ -- sin x = 1 ∨ tg x = − 3 ∨ tg x = 3 { } x ∈ π-, π-, 2π-, 4π-, 5π . 2 3 3 3 3

Rozwiązanie 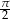π- 2 musimy jednak wyrzucić, bo nie należy do dziedziny równania (ze względu na 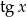tgx w równaniu).

Sposób II

Przekształcamy równanie (pozbywamy się tangensa).

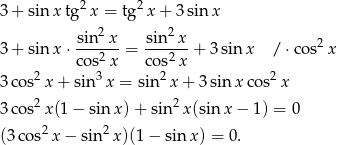
2 2 3 + sinx tg x = tg x + 3 sin x sin2 x sin2x 2 3 + sinx ⋅co-s2x = cos2x-+ 3sin x / ⋅cos x 2 3 2 2 3c os x + sin x = sin x + 3 sin x cos x 3c os2x(1 − sin x)+ sin 2x(sin x− 1) = 0 (3co s2x − sin2x )(1− sin x) = 0.

Wyrażenie w drugim nawiasie zeruje się dla 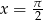x = π- 2 , ale liczba ta nie należy do dziedziny równania. Pozostaje więc równanie

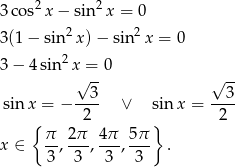
3co s2x − sin2x = 0 2 2 3(1 − sin x) − sin x = 0 3− 4sin2 x = 0 √ -- √ -- 3 3 sin x = − -2-- ∨ sin x = -2-- { } x ∈ π-, 2π-, 4π-, 5π . 3 3 3 3

Odpowiedź: { } π-, 2π, 4π-, 5π 3 3 3 3