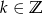Zadanie nr 5949751
Rozwiąż równanie 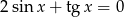 .
.
Rozwiązanie
Ze względu na tangens musi być 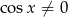 . Przekształcamy dane równanie
. Przekształcamy dane równanie
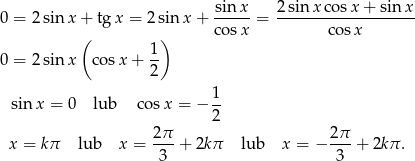
Odpowiedź: 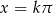 lub
lub 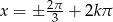 ,
, 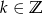
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 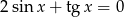 .
.
Ze względu na tangens musi być 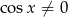 . Przekształcamy dane równanie
. Przekształcamy dane równanie
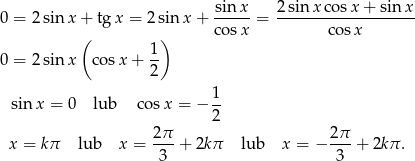
Odpowiedź: 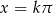 lub
lub 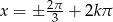 ,
,