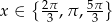/Szkoła średnia/Równania/Trygonometryczne/Z tangensem

Zadanie nr 6214745

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 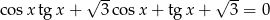√ -- √ -- co sxtg x + 3 cosx + tg x+ 3 = 0 w zbiorze ⟨0,2π ⟩ .

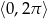Rozwiązanie

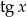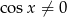Ze względu na tg x musi być oczywiście cosx ⁄= 0 .

Gdy się chwilę przyjrzymy, to można zauważyć, że w równaniu da się wyłączyć 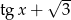√ -- tgx + 3 .

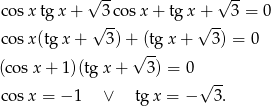
√ -- √ -- cosx tgx + 3 cos x+ tg x + 3 = 0 √ -- √ -- cosx (tg x + 3) + (tgx + 3 ) = 0 (co sx + 1)(tgx + √ 3) = 0 √ -- cosx = − 1 ∨ tgx = − 3.

Szkicujemy teraz wykresy cosinusa i tangensa.

PIC

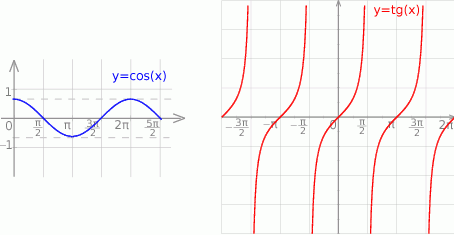
Z obrazków odczytujemy rozwiązania.

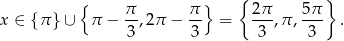
{ } { } x ∈ {π }∪ π − π,2 π − π- = 2π-,π , 5π . 3 3 3 3

 
Odpowiedź: { } x ∈ 2π,π , 5π 3 3

Wersja PDF