Zadanie nr 9288625
Rozwiąż równanie 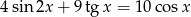 dla
dla 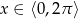 .
.
Rozwiązanie
Ze względu na tangens musi oczywiście być 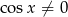 . Przekształcamy równanie.
. Przekształcamy równanie.
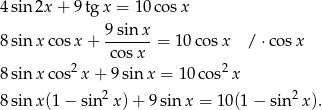
Widać, że możemy podstawić 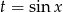 .
.
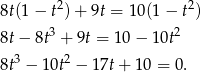
Teraz trudny moment, bo musimy znaleźć pierwiastek wymierny tego równania. Najpierw szukamy wśród dzielników wyrazu wolnego. Sprawdzając po kolei można znaleźć pierwiastek 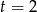 . Dzielimy teraz równanie przez
. Dzielimy teraz równanie przez 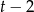 – my zrobimy to grupując wyrazy.
– my zrobimy to grupując wyrazy.
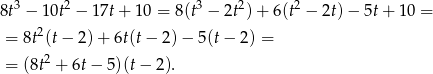
Rozwiązanie 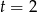 odpada, bo
odpada, bo 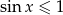 , więc pozostaje równanie
, więc pozostaje równanie
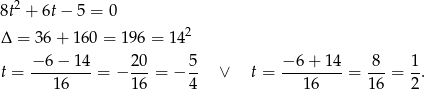
Pierwsze rozwiązanie odpada i otrzymujemy
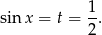
W przedziale 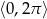 są dwa kąty spełniające ten warunek:
są dwa kąty spełniające ten warunek: 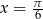 i
i 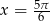 .
.
Odpowiedź: 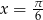 lub
lub