Zadanie nr 3101816
Rozwiąż równanie: 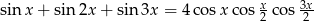 .
.
Rozwiązanie
Będziemy korzystać (żeby lewą stronę zamienić na iloczyn) ze wzorów
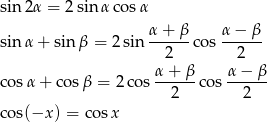
Przekształcamy lewą stronę
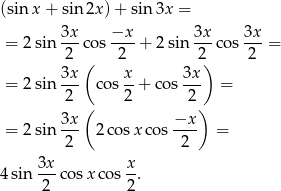
Podane równanie przyjmuje zatem postać
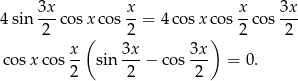
Mamy stąd 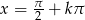 lub
lub 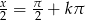 lub
lub 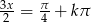 .
.
Odpowiedź: 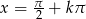 lub
lub 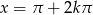 lub
lub 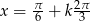
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie: 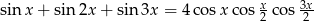 .
.
Będziemy korzystać (żeby lewą stronę zamienić na iloczyn) ze wzorów
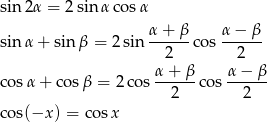
Przekształcamy lewą stronę
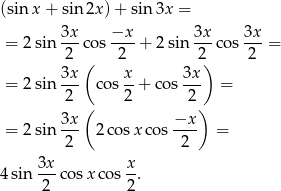
Podane równanie przyjmuje zatem postać
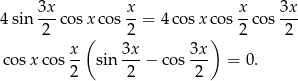
Mamy stąd 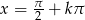 lub
lub 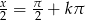 lub
lub 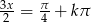 .
.
Odpowiedź: 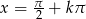 lub
lub 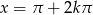 lub
lub