/Szkoła średnia/Równania/Trygonometryczne/Stopnia 3

Zadanie nr 7393187

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja 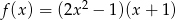2 f(x ) = (2x − 1)(x + 1)

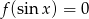  • Rozwiąż równanie f (sin x) = 0 .
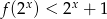  • Rozwiąż nierówność f(2x) < 2x + 1 .

Rozwiązanie

  • Przekształćmy wzór funkcji
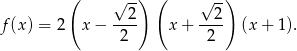
    ( √ -) ( √ --) 2 2 f (x) = 2 x − ---- x + ---- (x + 1). 2 2

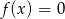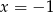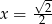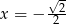    Zatem f(x) = 0 tylko dla x = − 1 , √ - x = --2 2 i √- x = − -2- 2 . Podane równanie sprowadza się więc do równań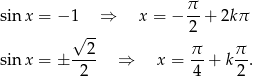

    π sin x = − 1 ⇒ x = − --+ 2kπ √ -- 2 --2- π- π- sin x = ± 2 ⇒ x = 4 + k 2.

     
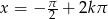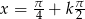    Odpowiedź: π x = − -2 + 2kπ lub x = π4 + kπ2- , k ∈ C .

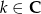  • Podstawiamy do podanego wzoru.
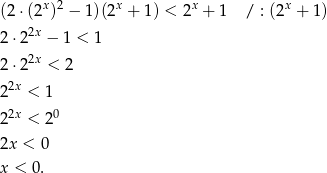
    x 2 x x x (2 ⋅(2 ) − 1)(2 + 1) < 2 + 1 / : (2 + 1) 2 ⋅22x − 1 < 1 2x 2 ⋅2 < 2 22x < 1 22x < 20 2x < 0 x < 0.

     
    Odpowiedź: x < 0

Wersja PDF