Zadanie nr 8526257
Rozwiąż równanie 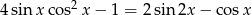 w przedziale
w przedziale 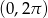 .
.
Rozwiązanie
Przekształcamy dane równanie
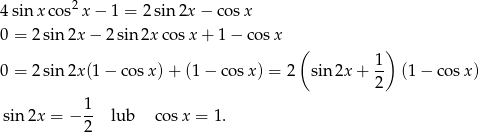
Szkicujemy sinusa i cosinusa.
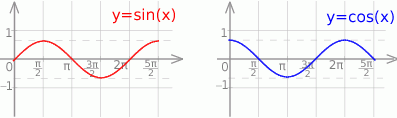
Druga równość jest sprzeczna w danym przedziale, a pierwsza daje
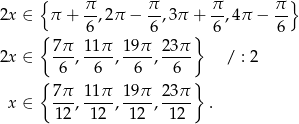
Odpowiedź: 
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 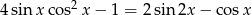 w przedziale
w przedziale 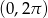 .
.
Przekształcamy dane równanie
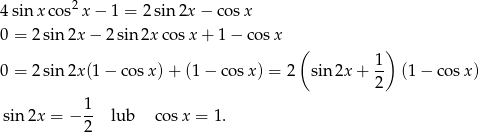
Szkicujemy sinusa i cosinusa.

Druga równość jest sprzeczna w danym przedziale, a pierwsza daje
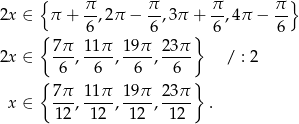
Odpowiedź: 
