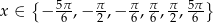Zadanie nr 9315611

Rozwiąż równanie

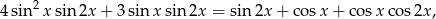
2 4 sin x sin 2x + 3 sin x sin 2x = sin 2x + cos x + cosx cos 2x,

dla 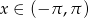x ∈ (− π,π ) .

Rozwiązanie

Zauważmy najpierw, że jeżeli rozpiszemy każdy 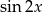sin 2x , to w równaniu łatwo będzie wyciągnąć 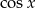co sx przed nawias.

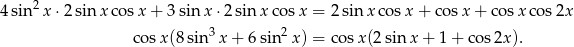
2 4sin x⋅ 2sinx cos x+ 3sin x⋅2 sinx cos x = 2 sin x cosx + cos x + cosx cos 2x cos x(8sin3 x+ 6sin2 x) = cos x(2sin x+ 1+ cos2x ).

Zatem 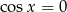co sx = 0 , czyli 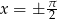x = ± π2- lub

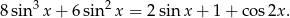
8 sin 3x + 6 sin 2x = 2 sin x + 1 + cos 2x.

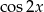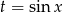Teraz rozpisujemy co s2x tak, aby móc podstawić t = sin x .

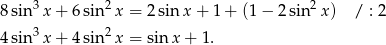
3 2 2 8sin x + 6 sin x = 2sin x+ 1+ (1− 2sin x ) / : 2 4sin3x + 4 sin2x = sin x + 1.

Podstawiamy 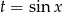t = sin x .

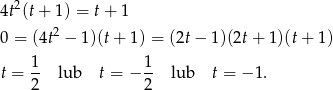
4t2(t+ 1) = t+ 1 0 = (4t2 − 1)(t + 1) = (2t − 1)(2t + 1)(t+ 1) t = 1- lub t = − 1- lub t = − 1. 2 2

Stąd

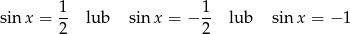
sinx = 1- lub sin x = − 1- lub sinx = − 1 2 2

Szkicujemy teraz wykres sinusa.

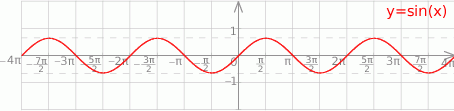
Z wykresu odczytujemy rozwiązania.

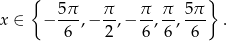
{ } x ∈ − 5-π ,− π-,− π, π-, 5π . 6 2 6 6 6

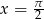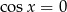Musimy jeszcze pamiętać o dodaniu rozwiązania x = π2- dla którego cosx = 0 .
Odpowiedź: x ∈ { − 5π,− π-,− π, π-, π-, 5π} 6 2 6 6 2 6