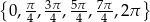Zadanie nr 9837378

Rozwiąż równanie 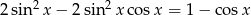2 2 2sin x− 2sin xcos x = 1 − cos x w przedziale ⟨0,2π ⟩ .

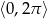Rozwiązanie

Przekształcamy dane równanie

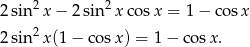
2 2 2sin x− 2sin xcos x = 1 − cos x 2sin2 x(1 − cosx ) = 1− cosx .

Otrzymujemy w ten sposób rozwiązanie 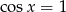cosx = 1 , czyli 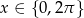x ∈ {0,2π } . Jeżeli natomiast 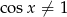cos x ⁄= 1 to dzielimy równanie stronami przez 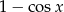1 − co sx i mamy

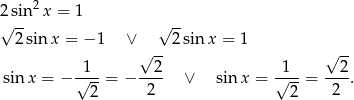
2 2√sin x = 1 √ -- 2sin x = − 1 ∨ 2 sin x = 1 √ -- √ -- -1-- --2- -1-- --2- sin x = − √ 2-= − 2 ∨ sin x = √ 2-= 2 .

Szkicujemy sinusa

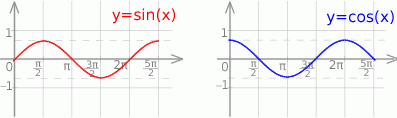
Z rysunku widać, że otrzymujemy dodatkowo rozwiązania

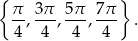
{ } π-, 3-π, 5π-, 7π . 4 4 4 4

Odpowiedź: { } 0, π-, 3π, 5π-, 7π,2π 4 4 4 4

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz