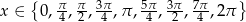/Szkoła średnia/Równania/Trygonometryczne/Stopnia 4

Zadanie nr 5983237

Rozwiąż równanie 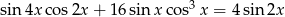3 sin4x co s2x + 16 sin x cos x = 4sin 2x w przedziale ⟨0,2π ⟩ .

Wersja PDF

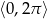Rozwiązanie

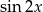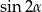Jeżeli się chwilę przyjrzymy, to można dostrzec, że z każdego składnika równania można wyłączyć sin 2x (korzystamy ze wzoru na sin 2α ).

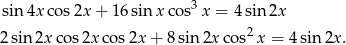
3 sin 4x cos2x + 16sin xco s x = 4 sin 2x 2 sin 2x cos 2xco s2x + 8 sin 2x cos2x = 4sin 2x.

Zatem albo 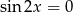sin2x = 0 , co daje 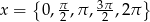{ π- 3π- } x = 0,2 ,π, 2 ,2π , albo możemy równanie podzielić stronami przez 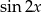sin 2x . Dzielimy.

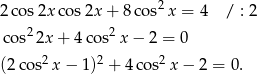
2 2 cos 2xco s2x + 8 cos x = 4 / : 2 cos22x + 4cos2 x− 2 = 0 2 2 2 (2 cos x − 1) + 4 cos x − 2 = 0.

Dalszą część rozwiązania dokończymy trzema sposobami.

Sposób I

Przekształcamy równanie.

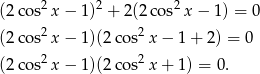
2 2 2 (2 cos x − 1) + 2(2 cos x − 1 ) = 0 (2 cos2x − 1)(2 cos2x − 1 + 2 ) = 0 2 2 (2 cos x − 1)(2 cos x + 1 ) = 0.

Wyrażenie w drugim nawiasie jest zawsze dodatnie, więc pozostaje równanie

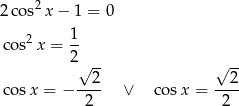
2cos2 x− 1 = 0 cos2 x = 1- 2√ -- √ -- 2 2 cos x = − ---- ∨ cosx = ---- 2 2

Szkicujemy cosinus.

PIC

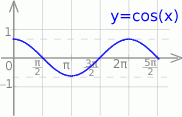
Z wykresu odczytujemy rozwiązania

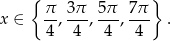
{ } x ∈ π-, 3-π , 5π-, 7π . 4 4 4 4

Pamiętamy, że do tych rozwiązań trzeba dodać wcześniej uzyskane rozwiązania równania 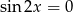sin 2x = 0 .

Sposób II

Podstawiamy 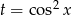t = co s2x .

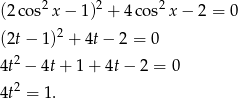
(2cos2 x− 1)2 + 4cos2 x− 2 = 0 2 (2t− 1 ) + 4t − 2 = 0 4t2 − 4t + 1 + 4t− 2 = 0 2 4t = 1.

Ponieważ 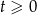t ≥ 0 mamy stąd 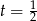t = 12 , czyli 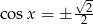√- co sx = ± 22- . Rozwiązania odczytujemy z wykresu tak jak w poprzednim sposobie.

Sposób III

Tak jak w I sposobie przekształcamy równanie do postaci

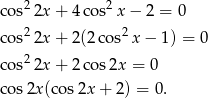
cos22x + 4cos2 x− 2 = 0 2 2 cos 2x + 2(2co s x − 1) = 0 cos22x + 2cos 2x = 0 cos 2x(cos 2x+ 2) = 0.

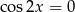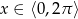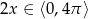Wyrażenie w nawiasie jest zawsze dodatnie, więc mamy cos2x = 0 . Teraz trzeba uważać, bo wprawdzie x ∈ ⟨0,2π ⟩ , ale 2x ∈ ⟨0,4π ⟩ . Mamy zatem

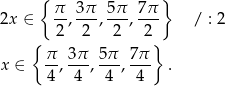
{ } π 3π 5π 7 π 2x ∈ --,---,---,--- / : 2 { 2 2 2 2} π- 3π- 5π- 7π- x ∈ 4 , 4 , 4 , 4 .

Pamiętamy, że do tych rozwiązań trzeba dodać wcześniej uzyskane rozwiązania równania 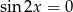sin 2x = 0 .  
Odpowiedź: { } x ∈ 0, π4, π2, 3π4-,π, 5π4-, 3π2 , 7π4-,2π

Wersja PDF