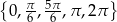Zadanie nr 9210911
Rozwiąż równanie 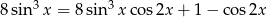 w przedziale
w przedziale 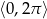 .
.
Rozwiązanie
Przekształcamy dane równanie
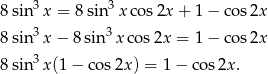
Jeżeli 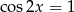 to
to 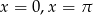 lub
lub 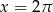 . Jeżeli natomiast
. Jeżeli natomiast 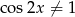 to możemy podzielić równanie stronami przez
to możemy podzielić równanie stronami przez 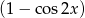 .
.
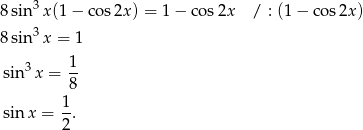
Otrzymujemy stąd dodatkowo 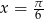 lub
lub 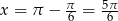 .
.
Odpowiedź: 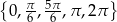
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 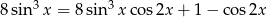 w przedziale
w przedziale 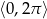 .
.
Przekształcamy dane równanie
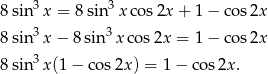
Jeżeli 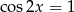 to
to 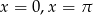 lub
lub 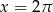 . Jeżeli natomiast
. Jeżeli natomiast 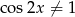 to możemy podzielić równanie stronami przez
to możemy podzielić równanie stronami przez 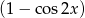 .
.
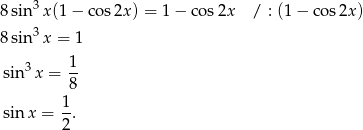
Otrzymujemy stąd dodatkowo 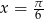 lub
lub 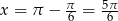 .
.
Odpowiedź: