/Szkoła średnia/Równania/Trygonometryczne/Stopnia 4

Zadanie nr 9531233

Wyznacz wszystkie rozwiązania równania 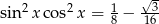2 2 1 √-3 sin x cos x = 8 − 16 należące do przedziału ⟨0,π⟩ .

Wersja PDF

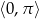Rozwiązanie

Będziemy korzystać ze wzorów

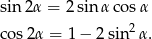
sin 2α = 2sin αcos α cos2 α = 1 − 2sin2 α.

Przekształcamy dane równanie

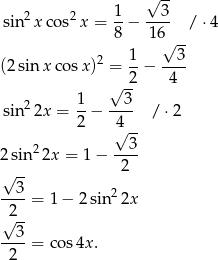
√ -- 2 2 1 3 sin xco s x = -− ---- / ⋅4 8 1 6√ -- (2 sin x cosx)2 = 1-− --3- 2 4 1 √ 3- sin2 2x = -− ---- / ⋅2 2 4√ -- 2 --3- 2 sin 2x = 1 − 2 √ -- --3-= 1− 2sin2 2x 2-- √ 3 ----= cos4x . 2

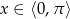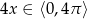W tym momencie musimy być ostrożni, bo wprawdzie x ∈ ⟨0,π ⟩ , ale wtedy 4x ∈ ⟨0,4π⟩ .

PIC

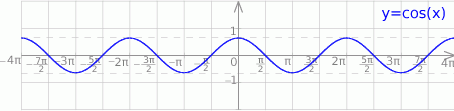
Rozwiązaniem powyższego równania są więc liczby

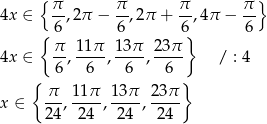
{ π π π π } 4x ∈ --,2π − --,2π + --,4π − -- { 6 6 6} 6 4x ∈ π-, 11π-, 1-3π , 23π / : 4 6 6 6 6 { } x ∈ π-, 11π-, 13π-, 23-π 24 24 24 24

 
Odpowiedź: { } x ∈ π-, 11π , 13π-, 23π 24 24 24 24

Wersja PDF