/Studia/Algebra liniowa/Macierze/Równania

Zadanie nr 8831560

Dodaj do ulubionych
Dodaj do rozwiązanych

Znaleźć macierz 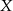X spełniającą równanie 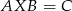AXB = C jeżeli

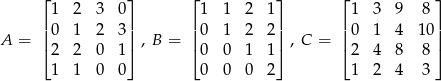
⌊1 2 3 0⌋ ⌊ 1 1 2 1⌋ ⌊1 3 9 8 ⌋ | | | | | | A = |0 1 2 3| , B = | 0 1 2 2| , C = |0 1 4 10| ⌈2 2 0 1⌉ ⌈ 0 0 1 1⌉ ⌈2 4 8 8 ⌉ 1 1 0 0 0 0 0 2 1 2 4 3

Rozwiązanie

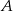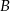Zaczniemy od wyznaczenia macierzy odwrotnych do A i B . Zrobimy to metodą ’lusterko’. Będziemy przekształcać macierz 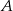A , wykonując operacje na wierszach tak, aby dostać macierz identyczności. Jednocześnie będziemy te same operacje wykonywać na identyczności. Na koniec z prawej strony dostaniemy −1 A .

| ⌊ 1 2 3 0⌋ | ⌊1 0 0 0⌋ | | | | | | 0 1 2 3| | |0 1 0 0| ⌈ 2 2 0 1⌉ | ⌈0 0 1 0⌉ 1 1 0 0 | 0 0 0 1 W 3−2W1 ⌊ ⌋ | ⌊ ⌋W4−W 1 1 2 3 0 | 1 0 0 0 || 0 1 2 3|| | || 0 1 0 0|| ⌈ 0 − 2 − 6 1⌉ | ⌈ −2 0 1 0⌉ 0 − 1 − 3 0 | −1 0 0 1 W 1−2W2 | W 3+2W2 ⌊ ⌋ | ⌊ ⌋W4+W 2 | 1 0 − 1 − 6| | | 1 − 2 0 0 | | 0 1 2 3 | | | 0 1 0 0 | ⌈ 0 0 − 2 7 ⌉ | ⌈− 2 2 1 0 ⌉ 0 0 − 1 3 | − 1 1 0 1 W 4/ (− 1) ⌊ ⌋ | ⌊ W⌋ 3↔W 4 1 0 − 1 − 6 | 1 −2 0 0 | 0 1 2 3 | | | 0 1 0 0 | |⌈ 0 0 1 − 3|⌉ | |⌈ 1 −1 0 −1 |⌉ | W1+W 3 0 0 − 2 7 | − 2 2 1 0 W 2−2W3 ⌊ ⌋ | ⌊ ⌋W 4+2W3 1 0 0 − 9 | 2 −3 0 −1 || 0 1 0 9 || | || − 2 3 0 2 || ⌈ 0 0 1 − 3⌉ | ⌈ 1 −1 0 −1 ⌉ 0 0 0 1 | 0 0 1 −2 W 1+9W4 | W 2−9W4 W 3+3W4
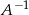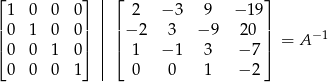
⌊ 1 0 0 0⌋ |⌊ 2 − 3 9 − 19⌋ | | || | | 0 1 0 0| || − 2 3 − 9 20 | = A −1 ⌈ 0 0 1 0⌉ |⌈ 1 − 1 3 − 7 ⌉ 0 0 0 1 | 0 0 1 − 2

Podobnie obliczamy 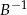B −1

⌊ ⌋ | ⌊ ⌋ 1 1 2 1 | 1 0 0 0 |0 1 2 2| | | 0 1 0 0| |⌈0 0 1 1|⌉ | |⌈ 0 0 1 0|⌉ | W1−W 2 0 0 0 2 | 0 0 0 1 W 2−2W 3 ⌊ ⌋ | ⌊ ⌋W4/2 1 0 0 − 1 | 1 − 1 0 0 || 0 1 0 0 || | || 0 1 − 2 0|| ⌈ 0 0 1 1 ⌉ | ⌈ 0 0 1 0⌉ 0 0 0 1 | 1 | 0 0 0 2 WW13+−WW 44 ⌊1 0 0 0⌋ | ⌊ 1 −1 0 1 ⌋ | | | | 2 | |0 1 0 0| | | 0 1 −2 01| = B −1 ⌈0 0 1 0⌉ | ⌈ 0 0 1 − 2⌉ 0 0 0 1 | 0 0 0 12 |

Mnożąc równanie 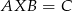AXB = C z lewej strony przez 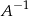−1 A i z prawej przez 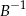−1 B mamy

⌊ ⌋ ⌊ ⌋ ⌊ 1 ⌋ 2 −3 9 − 1 9 1 3 9 8 1 − 1 0 2 X = A −1CB − 1 = || − 2 3 −9 2 0 || ⋅|| 0 1 4 10|| ⋅ ||0 1 − 2 0 || = ⌈ 1 −1 3 − 7 ⌉ ⌈ 2 4 8 8⌉ ⌈0 0 1 − 12 ⌉ 0 0 1 − 2 1 2 4 3 0 0 0 1 ⌊ ⌋ ⌊ 1 ⌋ ⌊ ⌋ 2 1 1 2 1 1 − 1 0 2 1 0 0 0 || 0 1 2 2|| ||0 1 − 2 0 || ||0 1 0 0 || = ⌈ 0 0 1 1⌉ ⋅ ⌈0 0 1 − 1 ⌉ = ⌈0 0 1 0 ⌉ 21 0 0 0 2 0 0 0 2 0 0 0 1
Wersja PDF