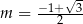/Szkoła średnia/Równania/Z wartością bezwględną/Wykładnicze/Z parametrem

Zadanie nr 4334344

Dla jakich wartości parametru 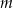m równanie 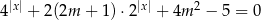|x| |x| 2 4 + 2(2m + 1) ⋅2 + 4m − 5 = 0 ma tylko jedno rozwiązanie?

Wersja PDF

Rozwiązanie

Jeżeli podstawimy 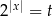|x| 2 = t to mamy równanie

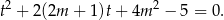
2 2 t + 2(2m + 1)t+ 4m − 5 = 0.

Jeżeli zapiszemy równość 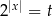|x| 2 = t w postaci

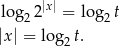
|x| log2 2 = log2t |x | = log t. 2

To widać, że równość ta da nam tylko jedną wartość x tylko dla

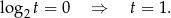
log t = 0 ⇒ t = 1. 2

Sprawdźmy, kiedy 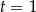t = 1 jest pierwiastkiem równania

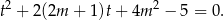
2 2 t + 2(2m + 1)t+ 4m − 5 = 0.

Podstawiamy 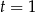t = 1

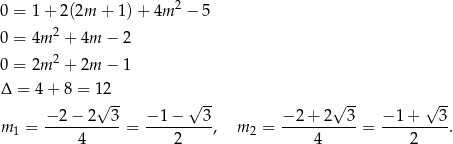
2 0 = 1 + 2(2m + 1) + 4m − 5 0 = 4m 2 + 4m − 2 2 0 = 2m + 2m − 1 Δ = 4+ 8 = 12 √ -- √ -- √ -- √ -- −-2−--2--3- −-1−----3- −-2-+-2---3 −-1-+---3- m 1 = 4 = 2 , m 2 = 4 = 2 .

Pozostała nam jeszcze jedna, niezbyt przyjemna rzecz, mianowicie sprawdzenie czy oprócz 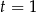t = 1 jest jeszcze jakiś dodatkowy pierwiastek dodatni (bo on może dać dodatkowe wartości x .). Najprościej jest to zrobić patrząc na wyraz wolny. Ponieważ

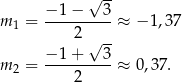
√ -- −-1−----3- m1 = 2 ≈ − 1,37 √ -- m2 = −-1+----3-≈ 0,37 . 2

oraz wyraz wolny jest równy

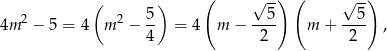
( ) ( √ -) ( √ --) 4m 2 − 5 = 4 m2 − 5- = 4 m − --5- m + --5- , 4 2 2

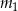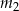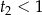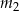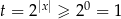łatwo sprawdzić, że dla m 1 wyraz wolny jest dodatni i mniejszy od 1, a dla m 2 jest ujemny. Na mocy wzorów Viéte‘a, oznacza to, że w pierwszej sytuacji jest dodatkowy pierwiastek dodatni t2 < 1 , a dla m 2 drugi pierwiastek jest ujemny. Pozostaje zauważyć, że w obu przypadkach ten dodatkowy pierwiastek nie prowadzi do dodatkowego pierwiastka wyjściowego równania, bo |x| 0 t = 2 ≥ 2 = 1 .  
Odpowiedź: 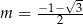√ - m = −-1−2--3 lub √ - m = −1+2--3-

Wersja PDF