/Szkoła podstawowa/Układy równań

Zadanie nr 9516527

Rozwiąż układ równań 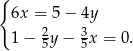{ 6x = 5 − 4y 1− 25y− 35x = 0.

Wersja PDF

Rozwiązanie

Liczymy

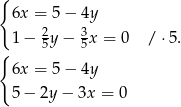
{ 6x = 5 − 4y 1 − 25y− 35x = 0 / ⋅5. { 6x = 5 − 4y 5 − 2y − 3x = 0

Sposób I

Podstawiamy 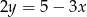2y = 5− 3x z drugiego równania do pierwszego.

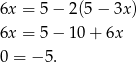
6x = 5 − 2(5 − 3x) 6x = 5 − 10 + 6x 0 = − 5.

Układ jest więc sprzeczny.

Sposób II

Dodajemy do pierwszego równania drugie pomnożone przez 2 i mamy

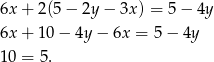
6x + 2(5− 2y− 3x) = 5 − 4y 6x + 10− 4y− 6x = 5 − 4y 10 = 5.

Układ jest więc sprzeczny.  
Odpowiedź: Układ jest sprzeczny.

Wersja PDF