/Studia/Algebra liniowa/Układy równań/Różne

Zadanie nr 3681283

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla podanego odwzorowania liniowego wyznaczyć zbiór tych wektorów 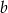b , dla których równanie 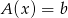A (x) = b ma rozwiązanie.

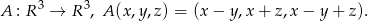
A : R 3 → R3, A (x,y,z) = (x − y,x + z,x − y + z ).

Rozwiązanie

Musimy ustalić jak wygląda obraz danego odwzorowania. Obraz ten jest rozpięty na wektorach 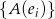{A (ei)} , gdzie 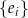{ei} są wektorami bazowymi w dziedzinie (będziemy oczywiście brać bazę standardową).

Liczymy

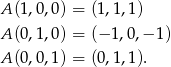
A (1,0,0) = (1,1,1) A (0,1,0) = (−1 ,0,− 1) A (0,0,1) = (0,1,1).

Zatem podane równanie ma rozwiązania dla wektorów 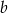b postaci

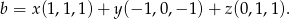
b = x (1,1,1)+ y(− 1,0,− 1) + z(0,1,1).

Na koniec możemy się zastanowić, czy to przedstawienie jest najprostsze możliwe, tzn. czy te trzy wektory generujące obraz 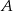A są liniowo niezależne. Aby to sprawdzić liczymy ich rząd (wstawiamy je do macierzy w kolumnach).

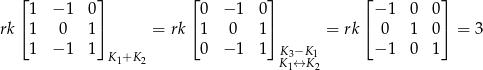
⌊ ⌋ ⌊ ⌋ ⌊ ⌋ 1 − 1 0 0 − 1 0 − 1 0 0 rk⌈ 1 0 1⌉ = rk ⌈1 0 1⌉ = rk⌈ 0 1 0⌉ = 3 1 − 1 1 K +K2 0 − 1 1 K3−K 1 − 1 0 1 1 K1↔K 2

 
Odpowiedź: 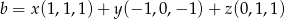b = x (1,1,1)+ y(− 1,0,− 1)+ z(0,1,1) dla x,y,z ∈ R

Wersja PDF