/Studia/Algebra liniowa/Układy równań/Różne

Zadanie nr 6846157

Dodaj do ulubionych
Dodaj do rozwiązanych

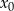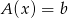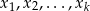Wykazać, że jeśli x 0 jest rozwiązaniem równania liniowego A (x) = b , a x1,x2,...,xk są rozwiazaniami równania liniowego jednorodnego stowarzyszonego, to 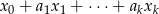x0 + a1x1 + ⋅⋅⋅+ akxk jest też rozwiązaniem równania A (x) = b .

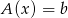Rozwiązanie

Liczymy

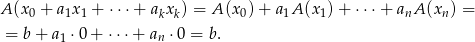
A (x + a x + ⋅⋅⋅ + a x ) = A (x ) + a A (x ) + ⋅⋅⋅+ a A (x ) = 0 1 1 k k 0 1 1 n n = b+ a1 ⋅0 + ⋅⋅⋅ + an ⋅ 0 = b.

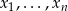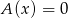Skorzystaliśmy z tego, że x1,...,xn są rozwiązaniami równania A (x) = 0 .

Wersja PDF