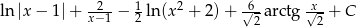/Studia/Analiza/Całki nieoznaczone/Wymierne

Zadanie nr 5108143

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę 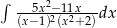∫ --5x2−-11x-- (x− 1)2(x2+2)dx .

Rozwiązanie

W mianowniku występuje czynnik liniowy w drugiej potędze i czynnik kwadratowy, zatem funkcja podcałkowa jest sumą dwóch ułamków prostych pierwszego rodzaju i ułamka prostego drugiego rodzaju

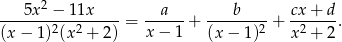
---5x2-−-11x----- --a--- ----b---- cx-+-d- (x− 1)2(x2 + 2) = x− 1 + (x − 1)2 + x 2 + 2 .

Mnożąc obie strony przez wspólny mianownik otrzymujemy

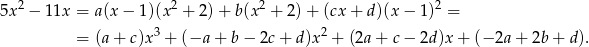
5x2 − 11x = a(x− 1)(x2 + 2) + b(x2 + 2) + (cx + d)(x − 1)2 = 3 2 = (a+ c)x + (−a + b − 2c + d)x + (2a + c − 2d )x+ (−2a + 2b+ d).

Porównując współczynniki otrzymujemy układ równań

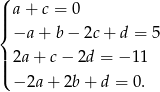
( a+ c = 0 |||{ −a + b− 2c+ d = 5 | 2a + c− 2d = − 11 ||( − 2a+ 2b + d = 0.

Podstawiając 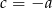c = −a z pierwszego równania do pozostałych trzech otrzymujemy układ

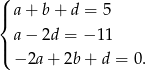
( |{ a+ b+ d = 5 a− 2d = − 11 |( − 2a+ 2b + d = 0.

Podstawiamy teraz 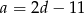a = 2d − 11 do pierwszego i trzeciego równania.

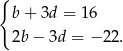
{ b + 3d = 16 2b − 3d = − 22.

Dodając te dwa równania stronami otrzymujemy 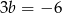3b = − 6 , czyli 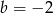b = − 2 . Stąd 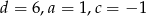d = 6,a = 1,c = − 1 . Mamy więc

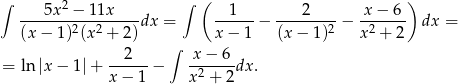
∫ 2 ∫ ( ) ---5x--−-11x----dx = --1---− ---2----− x-−-6-- dx = (x− 1)2(x2 + 2) x − 1 (x− 1)2 x2 + 2 2 ∫ x − 6 = ln |x− 1|+ ------− -2----dx. x− 1 x + 2

Ostatnią całkę liczymy osobno, korzystając ze wzoru

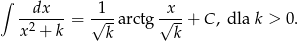
∫ --dx---= √1--arctg √x--+ C, dla k > 0. x 2 + k k k

Liczymy

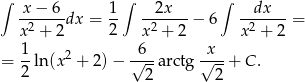
∫ x − 6 1 ∫ 2x ∫ dx -2----dx = -- -2-----− 6 -2-----= x + 2 2 x + 2 x + 2 = 1-ln(x2 + 2) − √6--arctg √x-+ C. 2 2 2

Mamy więc

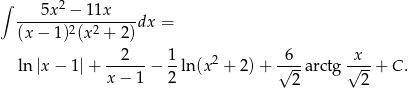
∫ ----5x2-−-11x---- (x − 1 )2(x2 + 2)dx = ln |x− 1|+ --2---− 1-ln(x2 + 2)+ √6--arctg√x--+ C. x− 1 2 2 2

 
Odpowiedź: ln |x − 1|+ --2-− 1ln(x 2 + 2) + √6-a rc tg √x-+ C x− 1 2 2 2

Wersja PDF