/Studia/Analiza/Całki nieoznaczone/Trygonometryczne

Zadanie nr 4059684

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę 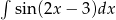∫ sin(2x − 3)dx .

Rozwiązanie

Sposób I

Wiemy, że całka z sinusa to minus cosinus. Zatem spodziewamy się wyniku postaci 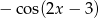− cos(2x − 3) . Jeżeli jednak policzymy pochodną z tej funkcji, to otrzymamy 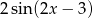2sin(2x − 3) . Musimy więc z przodu dodać 1 2 .

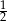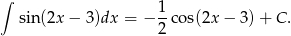
∫ 1 sin (2x− 3)dx = − -co s(2x− 3)+ C. 2

Sposób II

Podstawiamy 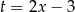t = 2x − 3 .

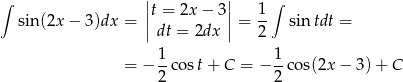
∫ | | ∫ ||t = 2x − 3|| 1- sin(2x − 3)dx = | dt = 2dx | = 2 sin tdt = = − 1-cost + C = − 1-cos(2x − 3) + C 2 2

 
Odpowiedź: 1 − 2 cos(2x − 3) + C

Wersja PDF