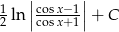Zadanie nr 4333003
Oblicz całkę 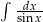 .
.
Rozwiązanie
Mnożymy licznik i mianownik wyrażenia podcałkowego przez 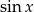 tak, aby móc podstawić
tak, aby móc podstawić 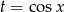 .
.
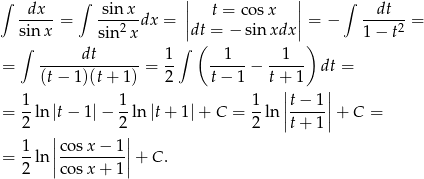
Odpowiedź: 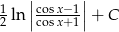
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 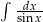 .
.
Mnożymy licznik i mianownik wyrażenia podcałkowego przez 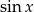 tak, aby móc podstawić
tak, aby móc podstawić 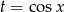 .
.
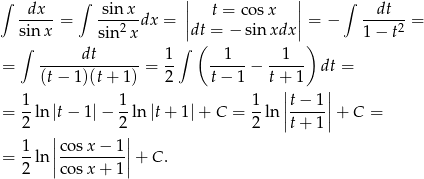
Odpowiedź: