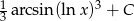Zadanie nr 6595455
Oblicz całkę 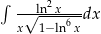 .
.
Rozwiązanie
Podstawiamy 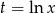 .
.
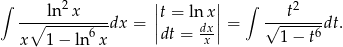
Teraz podstawiamy 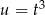 , aby otrzymać całkę
, aby otrzymać całkę 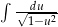 .
.
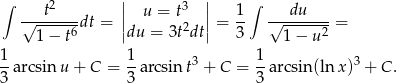
Odpowiedź: 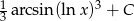
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 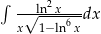 .
.
Podstawiamy 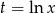 .
.
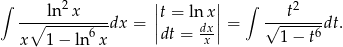
Teraz podstawiamy 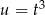 , aby otrzymać całkę
, aby otrzymać całkę 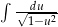 .
.
Odpowiedź: