Zadanie nr 9691793
Asia napisała na tablicy liczbę trzycyfrową, która jest podzielna przez 45, i w której zapisie występują tylko dwie różne cyfry. Jaką liczbę mogła napisać Asia? Podaj wszystkie możliwości.
Rozwiązanie
Sposób I
Wiemy, że szukana liczba ma dzielić się przez 45, więc musi dzielić się przez 9 i przez 5. W takim razie ostatnią cyfrą tej liczby musi być 0 lub 5, a ponadto suma cyfr musi dzielić się przez 9.
Jeżeli ostatnią cyfrą jest 0, to jest to liczba postaci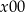 
lub 
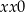. Ponieważ suma cyfr musi dzielić się przez 9 otrzymujemy w tym przypadku dwa rozwiązania: 900 i 990.
Jeżeli natomiast ostatnią cyfrą jest 5, to szukamy liczby w jednej z trzech postaci: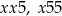 
lub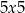 
. Suma cyfr podzielna przez 9 w pierwszym przypadku oznacza, że 
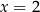, a dwóch kolejnych, że 
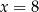. Mamy więc kolejne trzy rozwiązania: 225, 855, 585.
Sposób II
Liczb trzycyfrowych podzielnych przez 45 nie ma aż tak strasznie dużo, więc spróbujmy je wypisać.
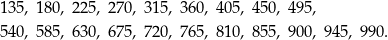
Widać teraz, że jest 5 liczb spełniających warunki zadania: 225, 585, 855, 900, 990
Odpowiedź: 225, 585, 855, 900, 990
