Zadanie nr 9850795
Uzasadnij, że dzieląc dowolną liczbę sześciocyfrową postaci 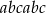 (np. 567567) przez 13, potem przez 11, a potem przez 7 otrzymamy liczbę trzycyfrową
(np. 567567) przez 13, potem przez 11, a potem przez 7 otrzymamy liczbę trzycyfrową 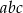 .
.
Rozwiązanie
Ponieważ
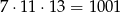
mamy
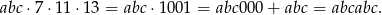
Zatem
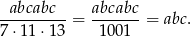
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uzasadnij, że dzieląc dowolną liczbę sześciocyfrową postaci 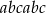 (np. 567567) przez 13, potem przez 11, a potem przez 7 otrzymamy liczbę trzycyfrową
(np. 567567) przez 13, potem przez 11, a potem przez 7 otrzymamy liczbę trzycyfrową 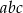 .
.
Ponieważ
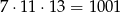
mamy
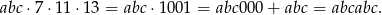
Zatem