/Szkoła średnia/Funkcje - wykresy/Parabola/Wzór z wykresu/1 niewiadoma

Zadanie nr 7542232

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja 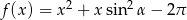2 2 f(x ) = x + xsin α− 2π , dla α ∈ ⟨0,2π ⟩ .

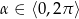  • Wyznacz wszystkie wartości parametru α , dla których osią symetrii wykresu tej funkcji jest prosta x = − 1 2 .
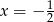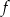  • Wykaż, że nie istnieje taka wartość parametru α , dla której do wykresu funkcji f należy punkt P = (1,− 2π ) .

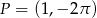Rozwiązanie

  • Ponieważ wykresem podanej funkcji jest parabola, więc wykres ten będzie symetryczny względem prostej 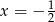x = − 1 2 wtedy i tylko wtedy, gdy pierwsza współrzędna wierzchołka tej paraboli jest równa 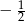1 − 2 . Mamy zatem równanie.: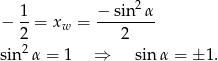
    2 − 1-= x = −-sin--α 2 w 2 sin 2α = 1 ⇒ sin α = ± 1.

    W podanym przedziale 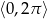⟨0,2π ⟩ są dwie takie wartości α :

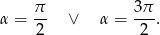
    π- 3π- α = 2 ∨ α = 2 .

     
    Odpowiedź: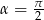 π α = 2- lub 3π α = -2-

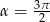
  • Wstawiamy podane wartości do wzoru i mamy
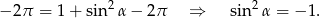
    2 2 − 2π = 1+ sin α− 2π ⇒ sin α = − 1.

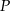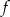    Równość ta jest oczywiście sprzeczna, co dowodzi, że punkt P nigdy nie jest punktem wykresu funkcji f .

Wersja PDF