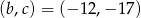/Szkoła średnia/Funkcje - wykresy/Parabola/Wzór z wykresu/2 niewiadome

Zadanie nr 3191184

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykresem funkcji kwadratowej 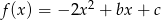2 f(x) = − 2x + bx + c jest parabola, której wierzchołkiem jest punkt 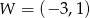W = (− 3,1) . Oblicz wartości współczynników 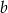b i c .

Rozwiązanie

Sposób I

Najprościej jest skorzystać z postaci kanonicznej 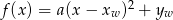2 f (x) = a(x − xw ) + yw . Podane współrzędne wierzchołka dają nam wzór

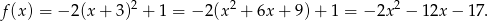
2 2 2 f(x) = − 2(x + 3 ) + 1 = −2 (x + 6x+ 9)+ 1 = − 2x − 12x − 1 7.

Zatem 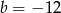b = − 12 i c = −1 7 .

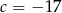Sposób II

Korzystamy ze wzoru na współrzędne

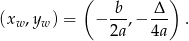
( ) -b- Δ-- (xw ,yw) = − 2a ,− 4a .

wierzchołka paraboli. Mamy zatem

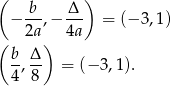
( ) b Δ − ---,− --- = (− 3,1) ( 2a ) 4a b- Δ- 4 ,8 = (− 3,1 ).

Mamy stąd 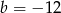b = − 12 oraz

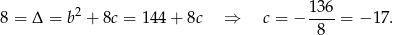
2 136 8 = Δ = b + 8c = 1 44+ 8c ⇒ c = − -8-- = − 17.

 
Odpowiedź: (b,c) = (− 1 2,− 17)

Wersja PDF