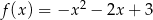/Szkoła średnia/Funkcje - wykresy/Parabola/Wzór z wykresu/3 niewiadome

Zadanie nr 5685862

Dodaj do ulubionych
Dodaj do rozwiązanych

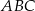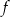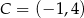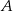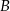Wierzchołki trójkąta ABC leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej f (zobacz rysunek). Pole tego trójkąta jest równe 8, punkt C = (− 1,4) jest wierzchołkiem paraboli, a punkty A i B leżą na osi 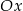Ox . Wyznacz wzór funkcji f .

PIC

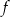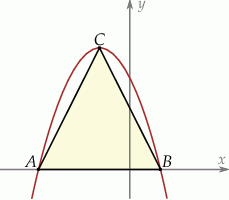
Rozwiązanie

Podane współrzędne wierzchołka paraboli oznaczają, że wysokość trójkąta 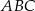ABC opuszczona na bok 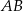AB ma długość 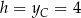h = yC = 4 . Stąd

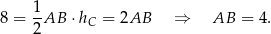
8 = 1AB ⋅hC = 2AB ⇒ AB = 4. 2

Wiemy ponadto, że osią symetrii danej paraboli jest prosta 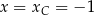x = xC = − 1 . W takim razie miejscami zerowymi funkcji 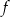f są liczby 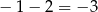− 1− 2 = − 3 i − 1 + 2 = 1 .

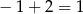Sposób I

Skoro znamy miejsca zerowe funkcji 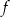f , to funkcja ta musi mieć wzór postaci

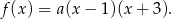
f(x ) = a(x − 1)(x + 3).

Współczynnik a wyznaczamy wstawiając współrzędne wierzchołka.

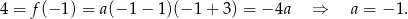
4 = f(− 1 ) = a(− 1− 1)(− 1+ 3) = − 4a ⇒ a = − 1 .

Mamy więc

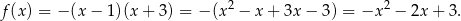
f (x) = − (x − 1)(x + 3) = − (x 2 − x + 3x − 3) = −x 2 − 2x + 3.

Sposób II

Znamy współrzędne wierzchołka paraboli, więc

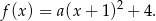
f (x) = a(x + 1)2 + 4.

Współczynnik a wyznaczamy podstawiając jedno z miejsc zerowych.

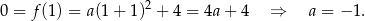
2 0 = f(1 ) = a(1+ 1) + 4 = 4a + 4 ⇒ a = −1 .

Stąd

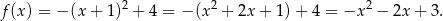
2 2 2 f (x) = − (x + 1) + 4 = − (x + 2x + 1 )+ 4 = −x − 2x+ 3.

 
Odpowiedź: 2 f (x) = −x − 2x + 3

Wersja PDF