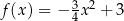Zadanie nr 6026101
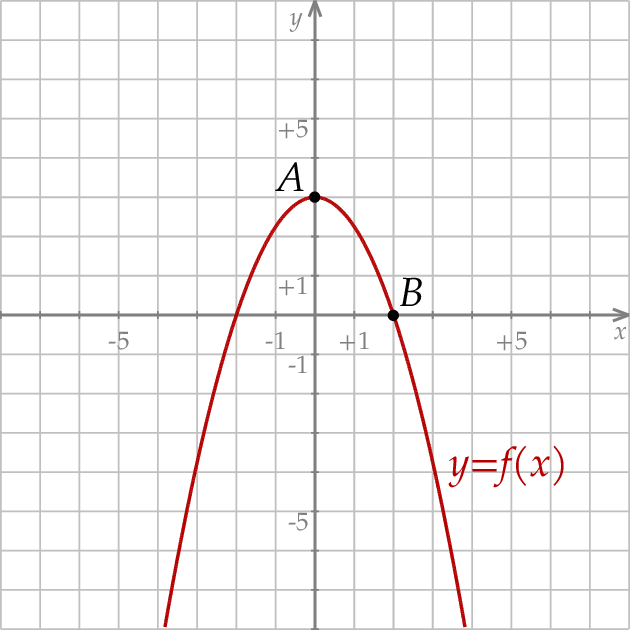
Wykresem funkcji kwadratowej  jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 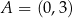 . Punkt
. Punkt 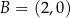 leży na wykresie funkcji
leży na wykresie funkcji 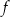 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 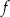 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
Sposób I
Wiemy, że wierzchołkiem paraboli będącej wykresem funkcji 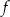 jest punkt
jest punkt 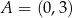 , więc funkcja
, więc funkcja 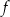 ma wzór postaci (postać kanoniczna)
ma wzór postaci (postać kanoniczna)
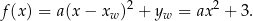
Współczynnik  wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 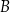 .
.
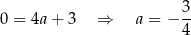
Zatem
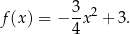
Sposób II
Osią symetrii danej paraboli jest prosta
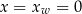
(czyli oś  ), więc jej drugim miejscem zerowym jest
), więc jej drugim miejscem zerowym jest 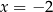 . Funkcja
. Funkcja 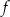 ma więc wzór postaci
ma więc wzór postaci
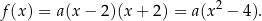
Współczynnik  wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 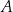 .
.
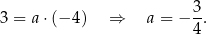
Funkcja  ma więc wzór
ma więc wzór
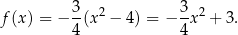
Odpowiedź: