/Szkoła średnia/Funkcje - wykresy/Parabola/Wzór z wykresu/3 niewiadome

Zadanie nr 6177880

Dodaj do ulubionych
Dodaj do rozwiązanych

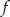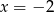Funkcja kwadratowa f dla x = − 2 przyjmuje wartość największą równą 1. Do wykresu funkcji 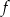f należy punkt 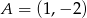A = (1,− 2) . Zapisz wzór funkcji kwadratowej f .

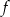Rozwiązanie

Z podanych informacji wiemy, że ramiona wykresu szukanej funkcji są skierowane dół, a wierzchołek jest w punkcie 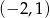(− 2,1 ) . Korzystając z postaci kanonicznej, zapisujemy funkcję 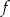f w postaci

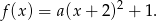
f (x) = a(x + 2)2 + 1.

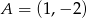Współczynnik a wyznaczamy z tego, że punkt A = (1 ,−2 ) należy do wykresu.

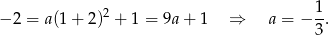
2 1 − 2 = a(1+ 2) + 1 = 9a + 1 ⇒ a = − 3.

Zatem

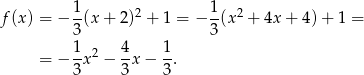
1- 2 1- 2 f(x ) = − 3(x + 2) + 1 = − 3(x + 4x + 4) + 1 = 1 4 1 = − -x 2 − -x − --. 3 3 3

Na koniec obrazek dla ciekawskich.

PIC

 
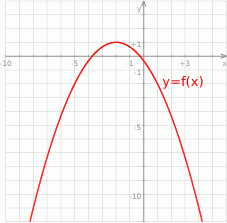
Odpowiedź: f(x ) = − 13(x + 2)2 + 1 = − 13x 2 − 43x− 13

Wersja PDF