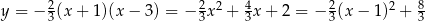/Szkoła średnia/Funkcje - wykresy/Parabola/Wzór z wykresu/3 niewiadome

Zadanie nr 9557258

Dodaj do ulubionych
Dodaj do rozwiązanych

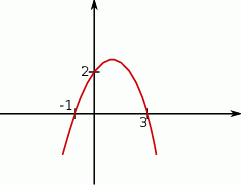
Na podstawie wykresu funkcji kwadratowej podaj jej wzór w postaci ogólnej, kanonicznej oraz iloczynowej.

PIC

Rozwiązanie

Sposób I

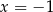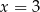Z wykresu widzimy, że miejscami zerowymi funkcji są liczby x = − 1 i x = 3 . Zatem szukana funkcja ma postać

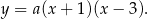
y = a(x + 1)(x − 3 ).

Współczynnik a wyznaczamy podstawiając współrzędne trzeciego z podanych punktów.

2- 2 = a(0+ 1)(0− 3) = − 3a ⇒ a = − 3.

Stąd

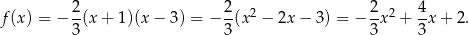
f(x) = − 2-(x + 1)(x − 3) = − 2(x2 − 2x − 3) = − 2x2 + 4x + 2. 3 3 3 3

Aby wyznaczyć postać kanoniczną zauważmy, że wierzchołkiem danej paraboli jest punkt o pierwszej współrzędnej 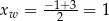−-1+-3 xw = 2 = 1 i drugiej

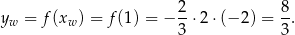
2 8 yw = f (xw) = f (1) = − --⋅2 ⋅(− 2) = --. 3 3

Postać kanoniczna jest więc równa

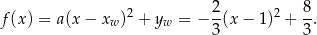
2 2- 2 8- f(x ) = a(x − xw ) + yw = − 3 (x− 1) + 3.

Sposób II

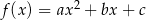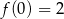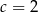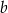Tym razem szukamy funkcji postaci f(x) = ax 2 + bx+ c . Z wykresu widać, że f (0) = 2 , czyli c = 2 . Współczynniki a i b wyznaczymy podstawiając współrzędne punktów 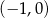(− 1,0) i (3,0) .

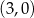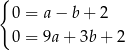
{ 0 = a − b + 2 0 = 9a + 3b + 2

Podstawiając 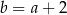b = a + 2 z pierwszego równania do drugiego, mamy

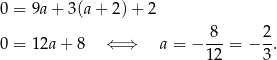
0 = 9a + 3(a + 2) + 2 8 2 0 = 12a + 8 ⇐ ⇒ a = − ---= − -. 12 3

Zatem 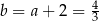4 b = a + 2 = 3 i szukana funkcja to

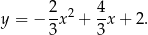
y = − 2-x2 + 4x + 2 . 3 3

Wyznaczamy jeszcze postać kanoniczną

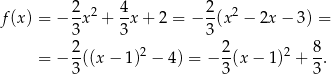
f(x ) = − 2x 2 + 4x + 2 = − 2(x2 − 2x − 3) = 3 3 3 2- 2 2- 2 8- = − 3((x − 1 ) − 4) = − 3(x − 1) + 3 .

i iloczynową

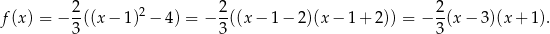
f(x) = − 2((x − 1)2− 4 ) = − 2((x − 1− 2)(x− 1+ 2)) = − 2(x − 3)(x + 1). 3 3 3

 
Odpowiedź: 2 2 2 4 2 2 8 y = − 3(x + 1)(x − 3) = − 3x + 3x + 2 = − 3(x− 1) + 3

Wersja PDF