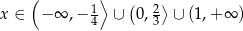Zadanie nr 3353963

Rozwiąż nierówność

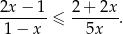
2x− 1 2 + 2x -------≤ -------. 1 − x 5x

Rozwiązanie

Dziedziną danej nierówności jest zbiór 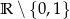R ∖ {0,1} . Przekształcamy nierówność w sposób równoważny.

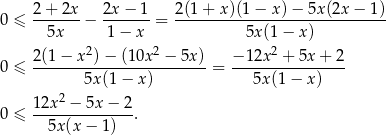
0 ≤ 2+--2x-− 2x-−--1 = 2-(1+-x-)(1−--x)−--5x(2x-−-1) 5x 1 − x 5x (1 − x ) 2(1 − x2) − (10x2 − 5x ) − 12x 2 + 5x + 2 0 ≤ ------------------------= ---------------- 5x(1 − x) 5x (1− x ) 12x2 − 5x − 2 0 ≤ --------------. 5x(x − 1)

Rozłóżmy teraz trójmian, który otrzymaliśmy w liczniku.

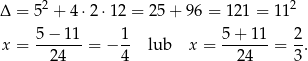
2 2 Δ = 5 + 4 ⋅2 ⋅12 = 25 + 9 6 = 121 = 11 5−--11- 1- 5-+-11- 2- x = 24 = − 4 lub x = 2 4 = 3 .

Interesującą nas nierówność możemy więc zapisać w postaci

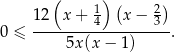
( ) ( ) 1 2 x + 1 x− 2 0 ≤ ---------4-------3-. 5x(x − 1 )

Przy założeniu 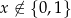x ⁄∈ {0,1} nierówność ta jest równoważna nierówności

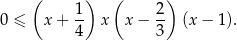
( 1) ( 2) 0 ≤ x+ -- x x− -- (x− 1). 4 3

Zaznaczamy miejsca zerowe otrzymanego wielomianu na osi.

Z rysunku odczytujemy rozwiązanie nierówności

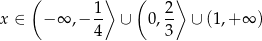
( ⟩ ( ⟩ x ∈ − ∞ ,− 1- ∪ 0, 2 ∪ (1,+ ∞ ) 4 3

Odpowiedź: ( ⟩ ( ⟩ x ∈ − ∞ ,− 1 ∪ 0, 2 ∪ (1,+ ∞ ) 4 3