/Szkoła średnia/Nierówności/Wymierne/Rozwiąż nierówność

Zadanie nr 8882931

Rozwiąż nierówność 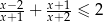x−-2 x+1- x+ 1 + x+2 ≤ 2 .

Wersja PDF

Rozwiązanie

Dziedziną danej nierówności jest zbiór 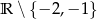R ∖ {− 2,− 1} . Przekształcamy nierówność w sposób równoważny.

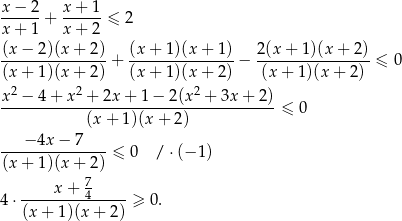
x−--2+ x-+-1-≤ 2 x+ 1 x + 2 (x − 2)(x+ 2) (x + 1)(x + 1) 2(x + 1)(x + 2) (x-+--1)(x+--2)-+ (x-+-1)(x-+-2)-− (x-+-1)(x-+-2-)-≤ 0 x2 −-4+-x-2 +-2x-+-1−--2(x2 +-3x-+-2)- (x + 1)(x + 2) ≤ 0 ---−4x-−--7----≤ 0 / ⋅(− 1) (x + 1)(x+ 2) x+ 7 4 ⋅---------4-----≥ 0. (x + 1)(x + 2 )

Równość w otrzymanej nierówności zachodzi tylko wtedy, gdy 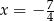x = − 74 . Pozostaje więc rozwiązać nierówność

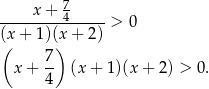
----x-+-74------ (x+ 1)(x+ 2) > 0 ( ) x+ 7- (x + 1)(x + 2) > 0. 4

Zaznaczamy miejsca zerowe otrzymanego wielomianu na osi.

PIC

Z rysunku odczytujemy rozwiązanie nierówności

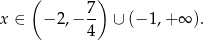
( ) x ∈ − 2,− 7- ∪ (−1 ,+∞ ). 4

Na koniec dodajemy znalezione wcześniej rozwiązanie: 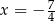x = − 74 .  
Odpowiedź: x ∈ (− 2,− 7⟩∪ (− 1,+ ∞ ) 4

Wersja PDF