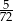Zadanie nr 1777404
Rzucamy trzy razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 12.
Rozwiązanie
Jeżeli o zdarzeniach elementarnych myślimy jak o ciągach wyników długości 3, to mamy
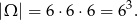
Policzmy zdarzenia sprzyjające. Liczbę 12 możemy napisać jako iloczyn trzech liczb na 3 sposoby:
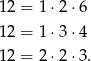
Aby policzyć liczbę zdarzeń sprzyjających musimy jednak uwzględnić fakt, że dla nas ważna jest kolejność wylosowanych liczb, czyli np. wyniki 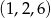 i
i 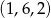 są różne.
są różne.
Jeden ze sposobów to wypisanie wszystkich możliwości:
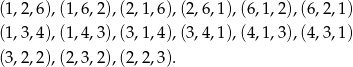
Inny sposób to zauważenie, że kolejność trzech liczb: 1,2,6 możemy ustalić na
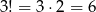
sposobów (ustalamy, która ma być pierwsza, i która druga). Podobnie jest z ustaleniem kolejności liczb 1,3,4. Kolejność liczb 2,2,3 można ustalić ma 3 sposoby (wybór miejsca dla 3).
W sumie jest więc 15 zdarzeń sprzyjających i prawdopodobieństwo wynosi
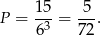
Odpowiedź: