Dane są trzy sześcienne kostki do gry: czerwona, niebieska i zielona. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że przy jednokrotnym rzucie trzema kostkami liczba otrzymana na niebieskiej kostce jest większa niż suma liczb otrzymanych na dwóch pozostałych kostkach.
Za zdarzenia sprzyjające przyjmijmy trójki wyrzuconych oczek, przy czym jako pierwszy będziemy zapisywać wynik otrzymany na niebieskiej kostce, jako drugi wynik otrzymany na czerwonej kostce, i wreszcie na końcu wynik z zielonej kostki. Mamy zatem
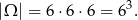
Policzmy ile jest zdarzeń sprzyjających.
Jeżeli na niebieskiej kostce wypadło 1 lub 2, to suma na pozostałych kostkach na pewno nie jest mniejsza, więc nie ma zdarzeń sprzyjających tego typu.
Jeżeli na niebieskiej kostce wypadło 3, to na pozostałych kostkach muszą być dwie jedynki, więc mamy w tym przypadku jedno zdarzenie sprzyjające:
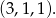
Wypisujemy zdarzenia sprzyjające z 4 na pierwszym miejscu
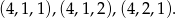
Teraz zdarzenia z 5 na pierwszym miejscu
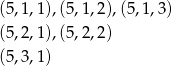
No i na koniec zdarzenia z 6 na pierwszym miejscu.
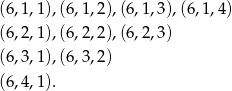
W sumie jest więc
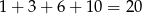
zdarzeń sprzyjających i prawdopodobieństwo wynosi
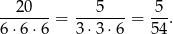
Odpowiedź: 
Informacje
Zadania
Losowe zadanie
