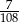Zadanie nr 9077132
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 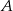 polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek otrzymanych w trzech rzutach będzie podzielny przez 48.
polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek otrzymanych w trzech rzutach będzie podzielny przez 48.
Rozwiązanie
O wynikach myślimy jak o parach otrzymanych oczek, czyli
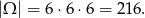
Zauważmy, że 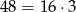 , więc jeżeli iloczyn otrzymanych oczek ma być równy 48, to przynajmniej jedna z otrzymanych liczb musi być podzielna przez 3 (czyli być równa 3 lub 6). Ponadto, jedna z liczb musi być równa 4, a pozostałe dwie to albo dwie liczby parzyste (czyli jedna z nich to 6), albo 4 i liczba podzielna przez 3 (bo tylko w ten sposób uzyskamy w rozkładzie
, więc jeżeli iloczyn otrzymanych oczek ma być równy 48, to przynajmniej jedna z otrzymanych liczb musi być podzielna przez 3 (czyli być równa 3 lub 6). Ponadto, jedna z liczb musi być równa 4, a pozostałe dwie to albo dwie liczby parzyste (czyli jedna z nich to 6), albo 4 i liczba podzielna przez 3 (bo tylko w ten sposób uzyskamy w rozkładzie 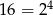 ). Zatem, nie uwzględniając kolejności, wylosowane liczby to
). Zatem, nie uwzględniając kolejności, wylosowane liczby to 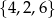 ,
, 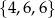 ,
, 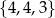 lub też
lub też 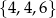 .
.
Wypiszmy zdarzenia sprzyjające.
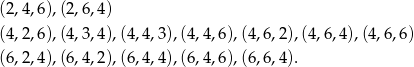
Zatem prawdopodobieństwo jest równe
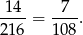
Odpowiedź: