/Szkoła średnia/Prawdopodobieństwo/Z definicji/Kostki/2 kostki

Zadanie nr 5701761

Dodaj do ulubionych
Dodaj do rozwiązanych

Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia 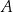A polegającego na tym, że w pierwszym rzucie wypadnie większa liczba oczek niż w drugim rzucie.

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.