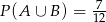Zadanie nr 9139117
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia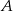 – na każdej kostce wypadła nieparzysta liczba oczek,
– na każdej kostce wypadła nieparzysta liczba oczek,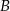 – suma wyrzuconych oczek jest nie mniejsza niż 8.
– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 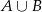 .
.
Rozwiązanie
Będziemy chcieli skorzystać ze wzoru
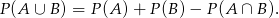
Na mocy powyższego wzoru, do obliczenia 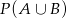 wystarczy obliczyć
wystarczy obliczyć 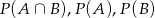 .
.
Najpierw obliczmy ile jest wszystkich zdarzeń elementarnych
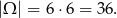
Wypiszmy zdarzenia sprzyjające 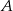
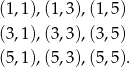
Zatem
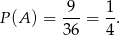
Wypiszmy zdarzenia sprzyjające 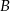
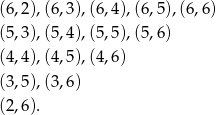
Zatem
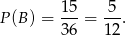
Zauważmy, że zdarzenia
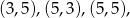
sprzyjają jednocześnie 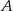 i
i 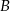 , więc
, więc
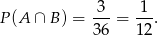
Pozostało to podstawić otrzymane wyniki
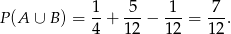
Odpowiedź: