/Szkoła średnia/Prawdopodobieństwo/Z definicji/Kostki/Nietypowe kostki

Zadanie nr 4288052

Dodaj do ulubionych
Dodaj do rozwiązanych

Na jednej kostce sześciennej znajdują się liczby: 2,3,3,6,6,6, a na drugiej: 1,1,4,6,7,7. Gra polega na rzucie wybraną kostką. Wygrywa ten, kto wyrzuci większą liczbę na swojej kostce. Masz prawo wyboru kostki. Którą kostkę należy wybrać, aby mieć większe szanse wygranej?

Rozwiązanie

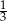Zauważmy, że rzucając pierwszą kostką wyrzucamy 2 z prawdopodobieństwem 16 , 3 z prawdopodobieństwem 13 i 6 z prawdopodobieństwem 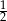12 . Podobnie dla drugiej kostki, możliwe wyniki to 1 z prawdopodobieństwem 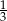1 3 , 4 i 6 z prawdopodobieństwem 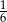1 6 , oraz 7 z prawdopodobieństwem 1 3 .

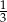Sposób I

Policzmy jakie są prawdopodobieństwa możliwych wyników (korzystamy z tego, że rzuty kostkami są niezależne).

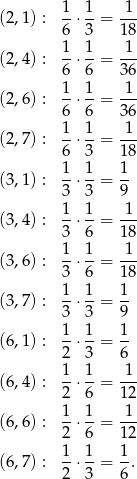
1 1 1 (2 ,1 ) : --⋅--= --- 6 3 18 (2 ,4 ) : 1-⋅ 1-= -1- 6 6 36 1 1 1 (2 ,6 ) : 6-⋅6-= 36- (2 ,7 ) : 1-⋅ 1-= -1- 6 3 18 1- 1- 1- (3 ,1 ) : 3 ⋅3 = 9 1 1 1 (3 ,4 ) : --⋅--= --- 3 6 18 (3 ,6 ) : 1-⋅ 1-= -1- 3 6 18 1 1 1 (3 ,7 ) : --⋅--= -- 3 3 9 (6 ,1 ) : 1-⋅ 1-= 1- 2 3 6 1- 1- -1- (6 ,4 ) : 2 ⋅6 = 12 1 1 1 (6 ,6 ) : --⋅--= --- 2 6 12 (6 ,7 ) : 1-⋅ 1-= 1. 2 3 6

Policzmy prawdopodobieństwo tego, że na pierwszej kostce jest więcej oczek:

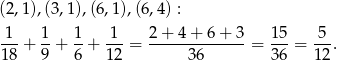
(2,1),(3,1),(6,1),(6,4 ) : 1 1 1 1 2 + 4 + 6 + 3 15 5 ---+ --+ --+ --- = ------------- = ---= --. 18 9 6 1 2 36 36 12

Ponieważ jest tylko jedna sytuacja, gdy jest remis (6,6), prawdopodobieństwo tego, że na drugiej kostce będzie większa liczba oczek jest równe

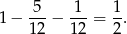
1 − -5-− 1--= 1. 12 12 2

Zatem lepiej jest wybrać drugą kostkę.

Sposób II

Patrząc na pierwszy sposób, trudno nie odnieść wrażenia, że niektóre rzeczy liczyliśmy niepotrzebnie. Tym razem od razu się zastanówmy kiedy liczba oczek na pierwszej kostce będzie większa niż na drugiej kostce. Zauważmy, że na pierwszej kostce możemy 2 zastąpić przez 3 i nie zmieni to sytuacji, zatem możemy przyjąć, że pierwsza kostka ma oczka 3,3,3,6,6,6. Zdarzenia sprzyjące to (3,1), (6,1) i (6,4). Prawdpodobieństwo takiego zdarzenia wynosi więc

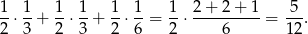
1 1 1 1 1 1 1 2 + 2 + 1 5 --⋅--+ -⋅ --+ --⋅--= --⋅----------= ---. 2 3 2 3 2 6 2 6 12

Prawdpodobieństwo zdarzenia przeciwnego liczymy jak poprzednio.  
Odpowiedź: Należy wybrać drugą kostkę.

Wersja PDF